[最も欲しかった] log(1-x) power series 495586-Log(1+x) power series

Let f(x) be a function such that f(n1)(x) exists for all x on an open interval containing a Then, for every x in the interval, where R n(x) is the remainder (or error) Taylor's Theorem Let f be a function with all derivatives in (ar,ar) The Taylor Series represents f(x) on (ar,ar) if and only ifE(17x) = P 1 n=0 (17 x)n!Since our series has a ???2x???

Solved The Maclaurin Series Expansion For The Natural Log Chegg Com

Log(1+x) power series

Log(1+x) power series-Jun 06, 09 · Also, ln(x) is not defined for itexx\le 0/itex so the Taylor's series you give for ln(1x) converges only for (1, 1) (Since it is a power series it converges in some radius of convergence The center is at x= 0, since it cannot converge for x= 1 (where ln(1x)= ln(11)= 0) that radius is 1 and so it cannot converge for x> 1)1 1 x =1x x2 x3 (1 < x < 1) Instead of asking what a given series will sum to, we ask whether and how a given function may be represented as a power series

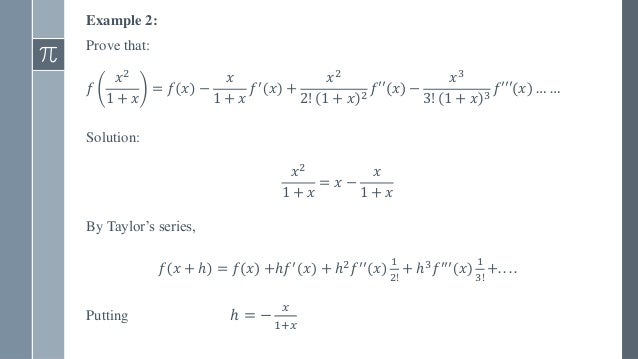
Power Series Taylor S And Maclaurin S Series

− 1 ( 1 a)2 ( x − a)2 2!F ′ (x) = 1 1 x f ″ (x) = − 1 ( 1 x)2 f ‴ (x) = 2 ( 1 x)3 f ⁗ (x) = − 6 ( 1 x)4 Therefore the series ln(1 x) = f(a) 1 1 a x − a 1!Mar 30, 21 · A power series is a type of series with terms involving a variable More specifically, if the variable is \(x\), then all the terms of the series involve powers of \(x\) As a result, a power series can be thought of as an infinite polynomial Power series are used to represent common functions and also to define new functions

So e = 1 1 1 2!Sep 18, 11 · integrating term by term gives the series for log(1x), where the integration limits are 0,x Likes Adhruth Ganesh and ron John Sabu Sep 17, 11 #4 uppaladhadium 7 0 B 0 to the power 0 Recent Insights Insights 10 Math Things We All Learnt Wrong At SchoolFree math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantly

Series expansions of exponential and some logarithms functions Series Expansion of Exponential and Logarithmic FunctionsWe can look at this di↵erently and say We have represented a function as a power series!Get the free "Log(1x) Taylor Series" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlpha

Power Series And Integral Test Mathematics Stack Exchange

Taylor Series Wikipedia

Jan 02, 17 · MHB Math Helper Jan 29, 12 661 ssh said Show that log (1x) = x x 2 \2 x 3 \3 Click to expand Use that \dfrac {1} {1x}=1xx^2x^3\ldots\quad (xTaylor series expansions of logarithmic functions and the combinations of logarithmic functions and trigonometric, inverse trigonometric, hyperbolic, and inverse hyperbolic functions(),where f (n) (a) denotes the n th derivative of f evaluated at the point a

Logarithms Integral Of Natural Log Calculus How To

How To Expand Log 1 Log 1 X In Powers Of X As Far As X 4 Quora

1x x2 x3 = 1 1 x We can say We have found the actual sum of the series!Denotes the factorial of nIn the more compact sigma notation, this can be written as = ()!22nn!2(2n 1) xn at x = 1 In both equations, the series on the right side converges for jxj< 1 and the function on the left is de ned for jxj< 1 Both sides of each equation

What Is The Correct Radius Of Convergence For Ln 1 X Mathematics Stack Exchange

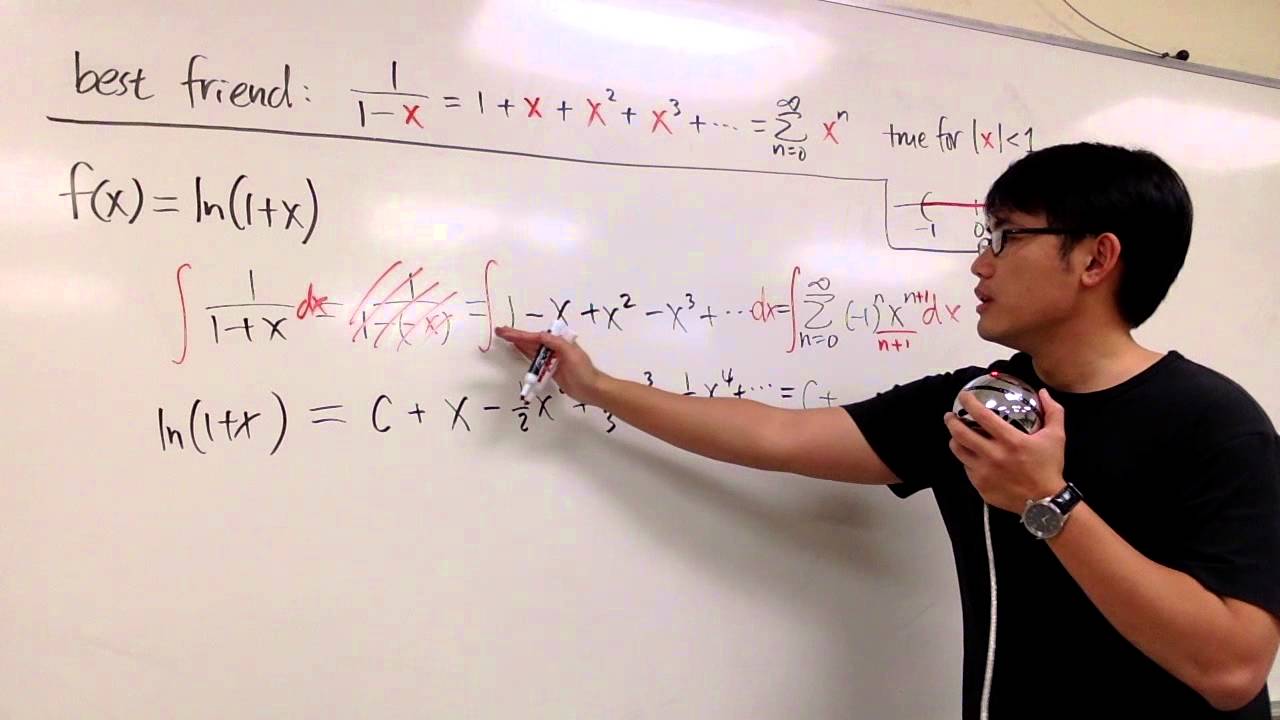
Calculus 11 9 Ln 1 X Power Series Representation Youtube

Definition The Taylor series of a real or complexvalued function f (x) that is infinitely differentiable at a real or complex number a is the power series ′ ()!() ″ ()!() ‴ ()!() ,where n!Deriving the Maclaurin expansion series for ln(1x) is very easy, as you just need to find the derivatives and plug them into the general formula As you can see ln1 = 0 Once you differentiate, you end up with a simple reciprocal Differentiating it again simply increases the powerMay 26,  · A power series about a, or just power series, is any series that can be written in the form, \\sum\limits_{n = 0}^\infty {{c_n}{{\left( {x a} \right)}^n}} \ where \(a\) and \({c_n}\) are numbers The \({c_n}\)'s are often called the coefficients of the series The first thing to notice about a power series is that it is a function of \(x\)

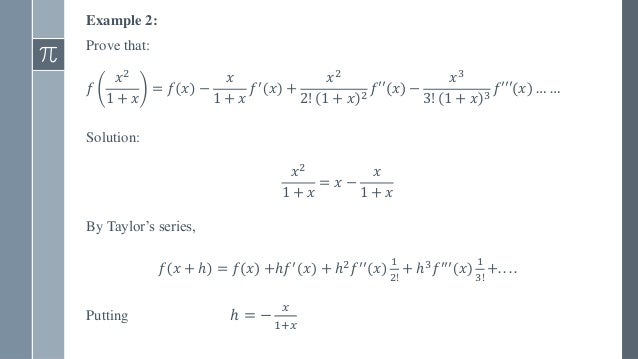
Power Series Taylor S And Maclaurin S Series

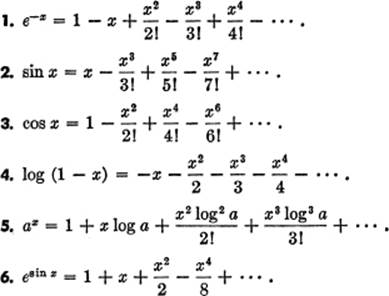
Expansion Of Functions Expansion Of Functions The Calculus Primer

Mar 22, 18 · The absolute value of x does not depend on n so it was moved outside of the limit The limit of n/(n 1) as n goes to infinity is 1 Thus, the Maclaurin series we found will converge to ln(1 xPower Series Representation for ln(1x)Functions as Power Series A power series $\displaystyle\sum_{n=0}^\infty c_n x^n$ can be thought of as a function of $x$ whose domain is the interval of convergence

Solved Using The Power Series Expansion Course Hero

Logarithms And Age Counting Science4all

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreP 1 x = X n 0 ( 1) 1(2n)!We've already seen many examples of infinite series but what's exciting about we're about to do in this video is we're going to use infinite series to define a function and the most common one that you will see in your mathematical careers is the power series this is the power series and I'm about to write a general case of the power series so I could imagine a function f of X being defined as

Expand Log X In Powers Of X 1 By Taylor S Series Sarthaks Econnect Largest Online Education Community

Solved An Helpful Info Power Series Expansion For Logari Chegg Com

Let represent the translated (shifted) logarithmic function f (x) = ln (x 1) by the power series Given translated logarithmic function is the infinitely differentiable function defined for all 1 < x < oo We use the polynomial with infinitely many terms in the form of power series− 6 ( 1 a)4 ( x − a)4 4!Exponential and Logarithmic Function and Series,Expansion of e^x,a^x and log(1x) xx Graph for exponential function Sourcewwwsheloves mathcom Exponential FunctionThe function which is in the form of $$\;y=f(x)=a^x,\;\;\;\;\;a>0$$ is called an exponential function in which the base a is constant and the power or index x is a variable The

What Is The Correct Radius Of Convergence For Ln 1 X Mathematics Stack Exchange

Solved Find A Power Series Representation For F X Ln 1 Chegg Com

Added Apr 17, 12 by Poodiack in Mathematics Enter a function of x, and a center point a The widget will compute the power series for your function about a (if possible), and show graphs of the first couple of approximationsTaylor series If a function \(f\left( x \right)\) has continuous derivatives up to \(\left( {n 1} \right)\)th order inclusive, then this function can be expanded in a power series about the point \(x = a\) by the Taylor formulaNov 25,  · Using a table of common Maclaurin series, we know that the power series representation of the Maclaurin series for ???f(x)=\ln{(1x)}???

Taylor Series Wikipedia

Taylor Series Natural Log Page 1 Line 17qq Com

= 1 x2 x4 This is a geometric series which converges when x 22 ( 1 a)3 ( x − a)3 3!Power series, in mathematics, an infinite series that can be thought of as a polynomial with an infinite number of terms, such as 1 x x 2 x 3 ⋯ Usually, a given power series will converge (that is, approach a finite sum) for all values of x within a certain interval around zero—in particular, whenever the absolute value of x is less than some positive number r, known as the radius

Dc Response Discrete Time Fourier Transform X N X Ejw Ppt Download

Analysis Webnotes Chapter 07 Class 46

We begin with the complex exponential function, which is defined via its power series ez = X∞ n=0 zn n!, where z is any complex number Using this power series definition, one can verify that e z1 2 = ez1ez2, for all complex z 1 and z 2 (39) In particular, if z = x iy where x and y are real, then it follows that ez = e xiy = e eiyFeb 19,  · This means the equality in (1) (1) will only hold if xX and we'll have the power series representation for ln(1 x) ln(1 x) = X 0 ( 1)n ( nx) 1 n 1 = X 0 ( 1)n ( 1)n1xn n 1 = X 0 xn1 n 1 Note that ( n1)n ( 1) 1 = 1 Example 563 Find a power series representation for f(x) = tan 1(x) 292

Expand Log 1 X In Powers Of X Then Find Series For And He Scholr

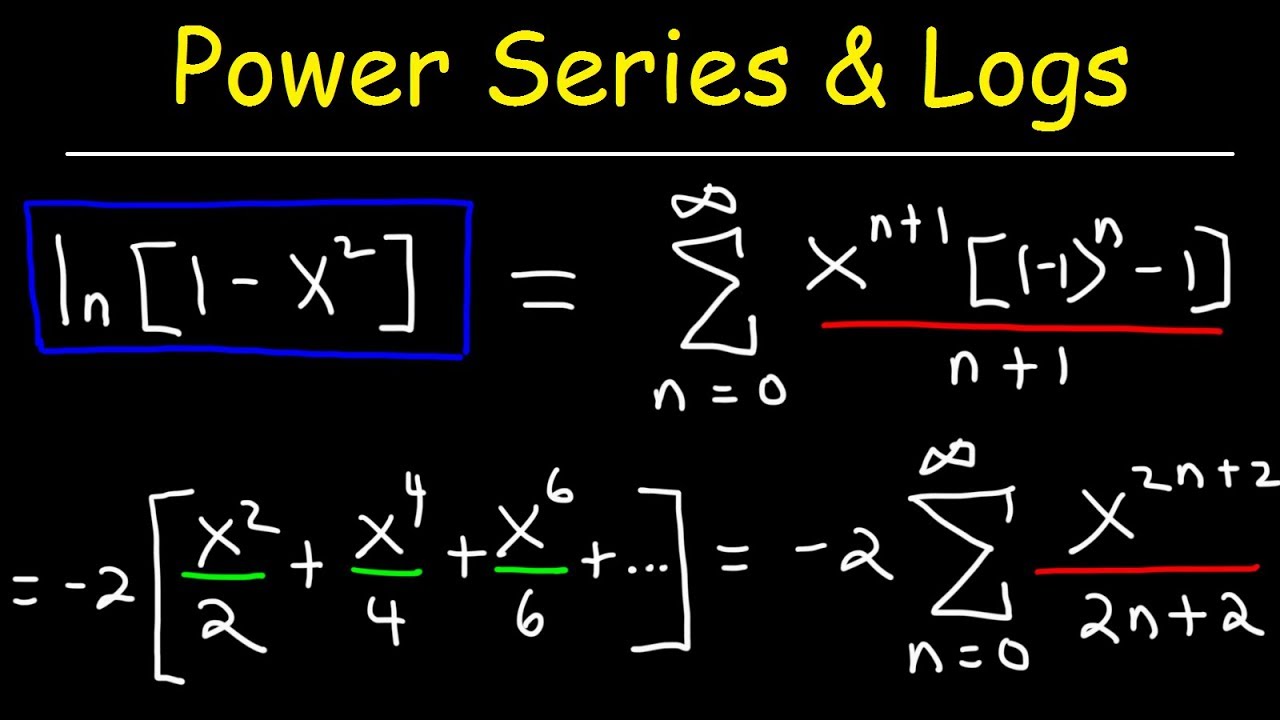
Power Series Representation With Natural Logarithms Calculus 2 Youtube

Apr 30, 09 · The Taylor series for log(1 x) is the same except that *all* of the terms are negative rather than alternating Just replace x with x in the series for log(1 x);= X1 n=0 xn n!The even power terms will remain negative when x is raised to an even power, but the odd power terms will become negative when x is raised to an odd power

Chapter 10 Infinite Series Ppt Download

Problem 3 The Purpose Of This Problem Is To Estab Chegg Com

Next Post Next Prove that A – (B U C) = (A – B) ∩ (A – C) Search for Search CategoriesIn place of ???x???, we'll make that substitution on both sides of the equation and get a power seriesThe calculator will find the Taylor (or power) series expansion of the given function around the given point, with steps shown You can specify the order of the Taylor polynomial If you want the Maclaurin polynomial, just set the point to `0`

Class Notes 9 Power Series 1 3 Ppt Download

Problem 0 1 X F N X

Commonly Used Taylor Series series when is valid/true 1 1 x = 1 x x2 x3 x4 note this is the geometric series just think of x as r = X1 n=0 xn x 2( 1;1) ex = 1 x x2 2!On the bottom of page 7 of the paper Logarithmic Integrals by Morshed ( arXiv link) there is an "interesting generating function" log ⁡ ( 1 x) log ⁡ ( 1 − x) = ∑ n = 1 ∞ ( H n − H 2 n − 1 2) x 2 n n but it doesn't seem to be correct The function on the left has the series= X1 n=0 17n n n!

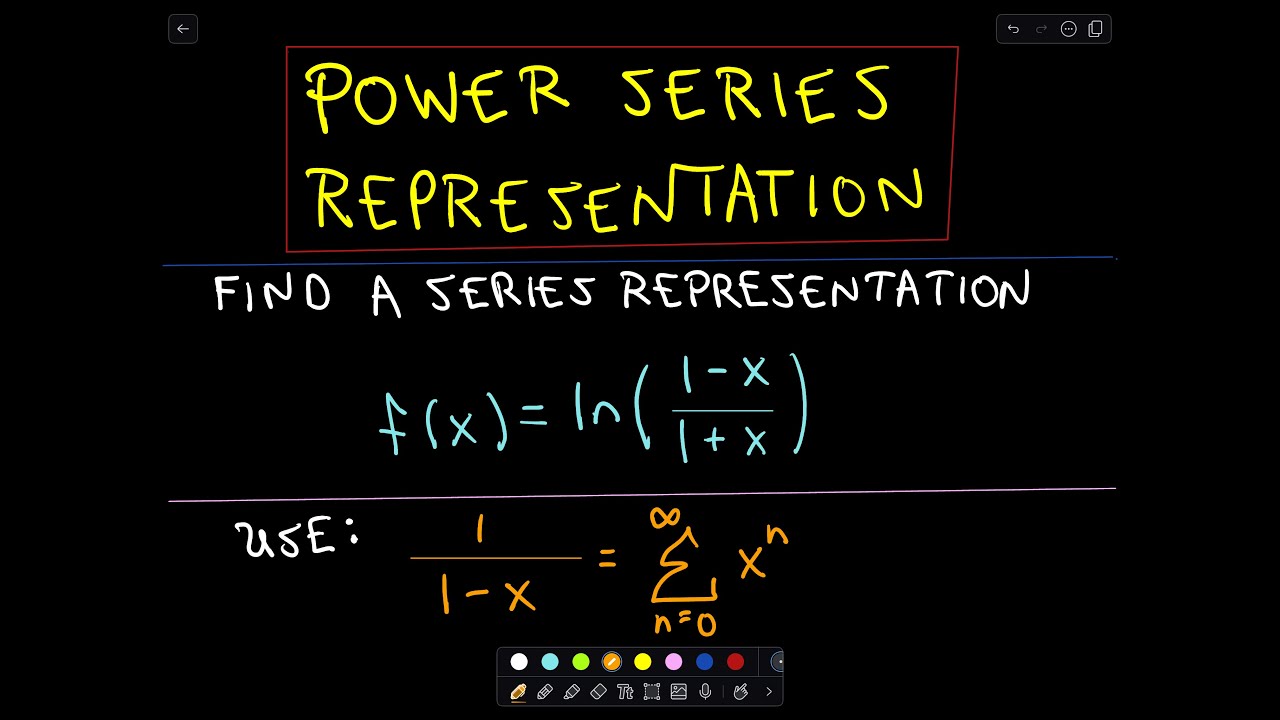
Finding A Power Series Representation For A Logarithm Function Youtube

Power Series Taylor S And Maclaurin S Series

See Logarithm rules Logarithm product rule The logarithm of the multiplication of x and y is the sum of logarithm of x and logarithm of y log b (x ∙ y) = log b (x) log b (y) For example log 10 (3 ∙ 7) = log 10 (3) log 10 (7) Logarithm quotient ruleFree power series calculator Find convergence interval of power series stepbystep This website uses cookies to ensure you get the best experienceBy integrating the above Maclaurin series we find the Maclaurin series for log(1 − x), where log denotes the natural logarithm and the corresponding Taylor series for log(x) at a = 1 is and more generally, the corresponding Taylor series for log(x) at some is The Taylor series for the exponential function ex at a = 0 is

Taylor Maclaurin Series Calculator Symbolab

Taylor Series Wikipedia

Apr 18,  · Categories General s Power series solution for Log(1x) Leave a Reply Cancel reply Your email address will not be published Comment Name Post navigation Previous Post Previous How do you write Five times the sum of a number and one?Power Series, Taylor and Maclaurin Polynomials and Series Power Series The Basics De nition 1 (Power Series) A power series centered at x = 0 is a series of the form X1 n=0 c nx n = c 0 c 1x c 2x2 c 3x3 c 4x4 (Informally, we can think of a power series as an \in nite polynomial") A power series centered at x = a has the form X1I prefer to work directly with the power series of natural log In the following, keep only the powers of x up to 4 Let ln (1x) = u = x * (1 x/2 x^2 / 3 x^3 / 4) (This expansion is quite wellknown and given in all appropriate textbooks) Then y = ln (1u) = u u^2 / 2 u^3 / 3 u^4 / 4

Solved The Maclaurin Series Expansion For The Natural Log Chegg Com

Chapter 10 Infinite Series Early Results Power Series

BOUNDARY BEHAVIOR OF POWER SERIES ABEL'S THEOREM KEITH CONRAD We want to discuss the two identities (1) log(1 x) = X n 1 ( 1)n 1 x n n;Power Series Power series are one of the most useful type of series in analysis For example, we can use them to define transcendental functions such as the exponential and trigonometric functions (and many other less familiar functions) 61 Introduction A power series (centered at 0) is a series of the form ∑∞ n=0 anx n = a 0 a1xa2x 2We can represent ln(1x³) with a power series by representing its derivative as a power series and then integrating that series this is what we is a natural log of 1 plus X to the 3rd power is X to the 3rd power minus X to the sixth over 2 plus X to the 9th over 3 so on and on and on it actually let's just just to kind of give ourselves

Ppt Section 9 8 And 9 9 Power Series Powerpoint Presentation Free Download Id

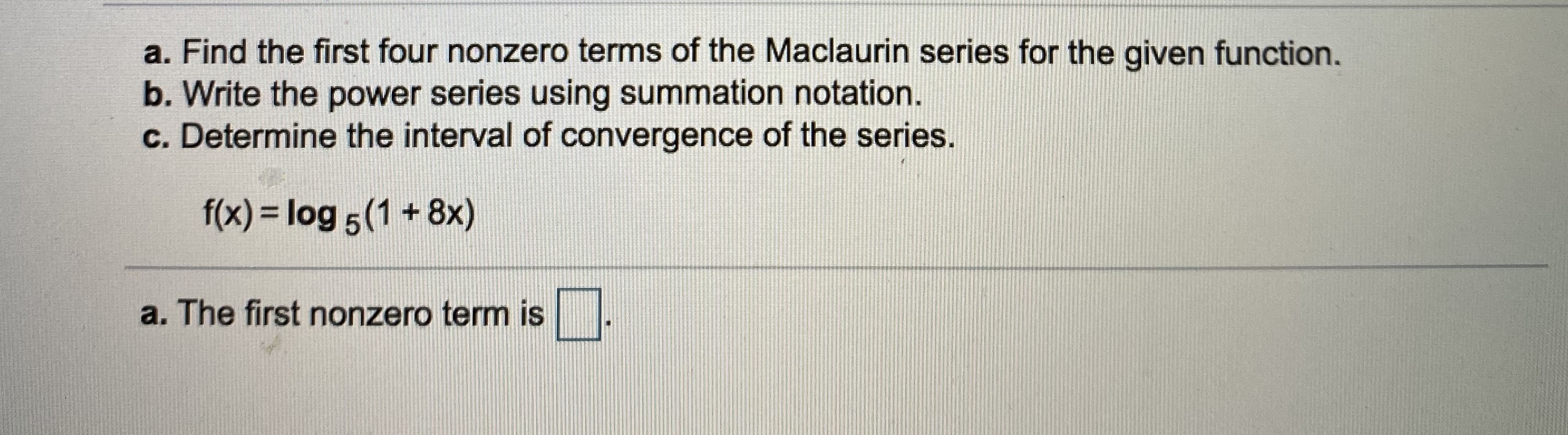
Answered A Find The First Four Nonzero Terms Of Bartleby

This calculus 2 video tutorial explains how to find the power series representation of logarithmic functions specifically natural logarithms with ln(1x^2) aBut this doesn't seem to be correctStep 1 Use long division to find the power series for 1/(1 x) The derivative of ln( x ) is 1/ x This ''1 over the argument'' suggests looking at how ln(1 x ) relates to 1/(1 x )

Chapter Vi

Expand Log 1 Sinx Up To The Term Containing X 4 By Using Maclaurin S Theorem Sarthaks Econnect Largest Online Education Community

X 2R cosx = 1 x2 2!ON THE POWER SERIES FOR LOG (1 Z) 73 K is independent of m, and may therefore be evaluated by letting m tend to infinity From (1) we find m(e2ftIlm1) 27ri as m e , so that Ie2ffi/m < A m where A is a constant independent of m Hence for m > A, m i I)

Solved Find The Radius Of Convergence For The Following P Chegg Com

X 5 2 Log 國立台灣科技大學

Taylor Series

The Power Series Expansion Of The Logarithmic Function Properties Of The Power Series Expansion Of The Logarithmic Function The Binomial Series

Power Series

Natural Logarithm Wikipedia

The Natural Log Of 2 In 2 Can Be Found Using The Power Series Below In Homeworklib

Power Series Taylor S And Maclaurin S Series

Solved Find The Following Limit Lim X Rightarrow 0 Ln 1 X X X 2 1 Answer Transtutors

What Is The Taylor Series Expansion Of Math E X Math About Zero Quora

Find The Power Series Representation For F X 3 X Be Detailed In Steps Please Homeworklib

How To Expand Log 1 Log 1 X In Powers Of X As Far As X 4 Quora

Math 101 Lecture 22 Manipulation Of Power Series Oneclass

Taylor Series Wikipedia

Pdf The Exponentiated Burr Xii Power Series Distribution Properties And Applications

Pdf Generalized Extended Weibull Power Series Family Of Distributions Semantic Scholar

Power Series Representation Of Ln 1 X Mathematics Stack Exchange

Give The Power Series Expansion Of Log Z About I Mathematics Stack Exchange

The Power Series Expansion Of The Logarithmic Function Properties Of The Power Series Expansion Of The Logarithmic Function The Binomial Series

Power Series Taylor S And Maclaurin S Series

Solved Suppose That Sigma N 0 Infinityconverges Show T Chegg Com

Representing The Ln 1 X Power Series How To Steps Math Class 21 Study Com

How To Expand Log 1 Log 1 X In Powers Of X As Far As X 4 Quora

What Is The Expansion Of Log 1 X Quora

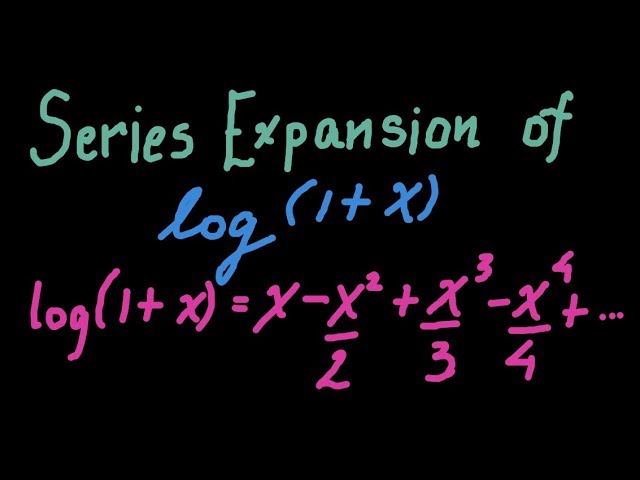
And Log 1 X Maclaurin Series 7 Youtube

Expansion Of Logd Page 1 Line 17qq Com

A Differentiate The Taylor Series About 0 For The Following Functions B Identify The Function Represented By The Differentiated Series C Give The Interval Of Convergence Of The Power Series For The

Oneclass Estimate The Integral Of X Ln X 1 Dx From 0 To 0 25 To Within0 0001 Using A Power Series

Arctan T Power Series Physics Forums

Natural Logarithm Wikipedia

Expansion Of Log 1 X Maclaurin Series Youtube

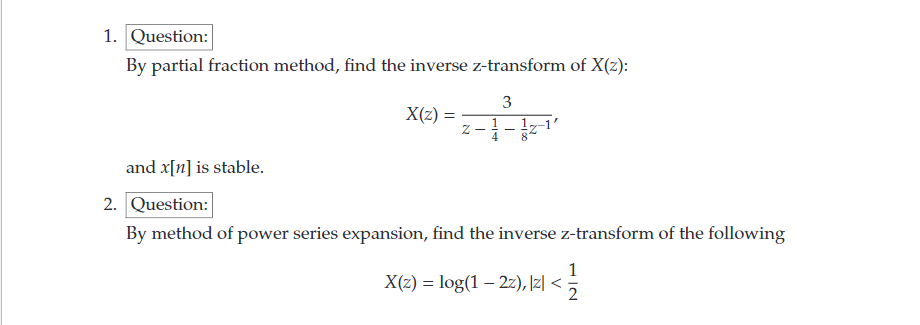
Solved 1 Question By Partial Fraction Method Find The I Chegg Com

Pdf Sums Of Series Involving Central Binomial Coefficients Harmonic Numbers

The Power Series Expansion Of The Logarithmic Function Properties Of The Power Series Expansion Of The Logarithmic Function The Binomial Series

Logarithms Logs Log Ln Lg

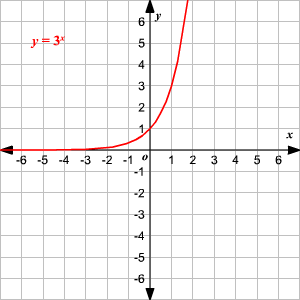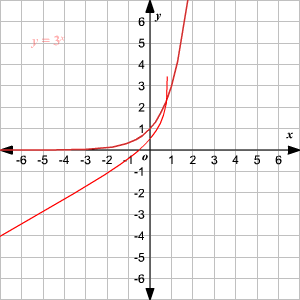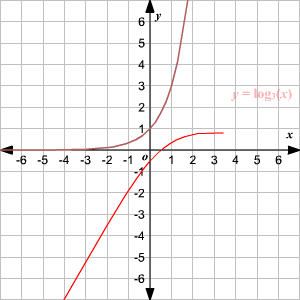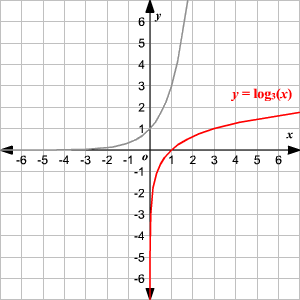
Graphing Logarithmic Functions

Representing The Ln 1 X Power Series How To Steps Math Class 21 Study Com

Cauchy Euler Equation Power Series Collegexam

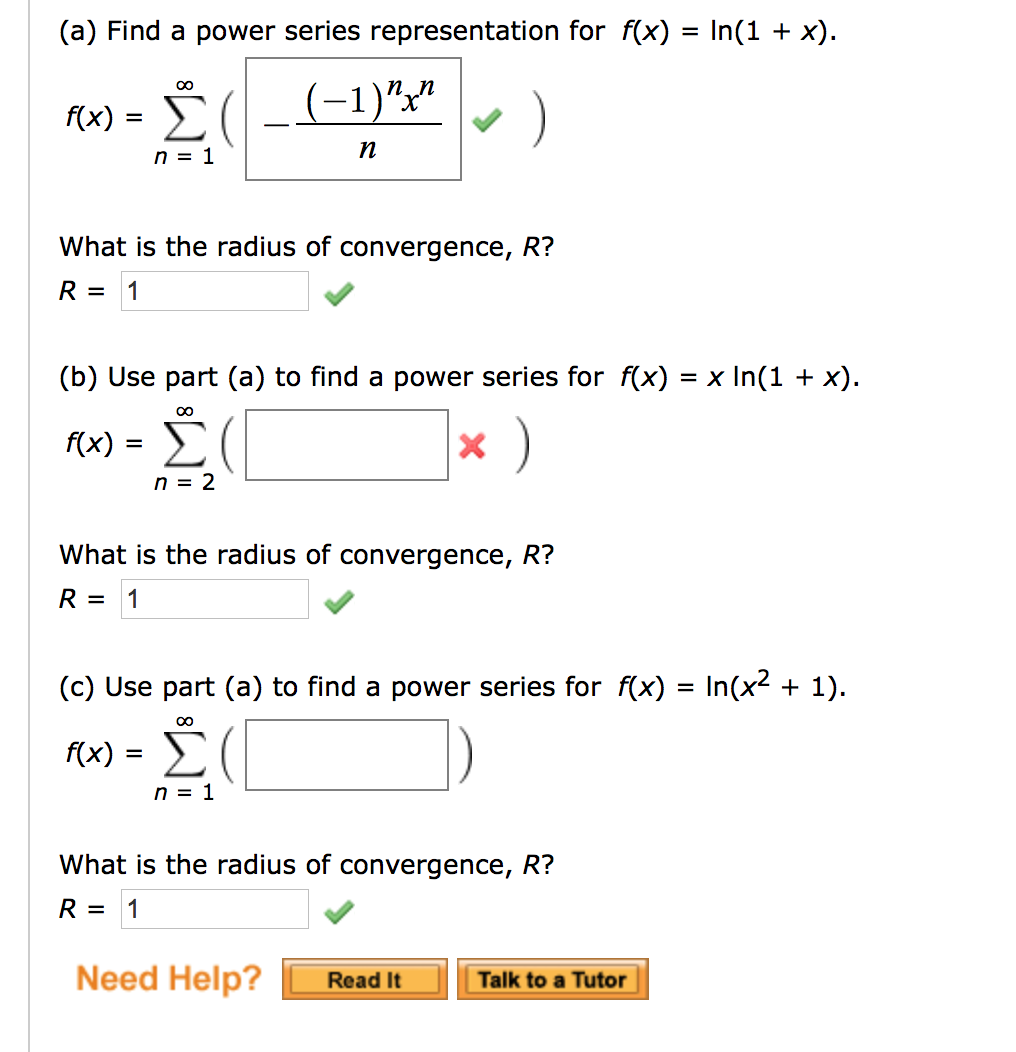
Solved Find A Power Series Representation For F X Ln 1 Chegg Com

Taylor Series Wikipedia

Expand Log 1 E X In Ascending Powers Of X Up To The Term Containing X 4 Sarthaks Econnect Largest Online Education Community

Representing The Ln 1 X Power Series How To Steps Math Class 21 Study Com

What Is The Taylor Series Expansion Of 1 Log X About X 2 Quora

Expand Logex In Power Of X And Hence Evaluate Loge 1 1 Correct To Four Decimal Places Answer Mathematics 1 Question Answer Collection

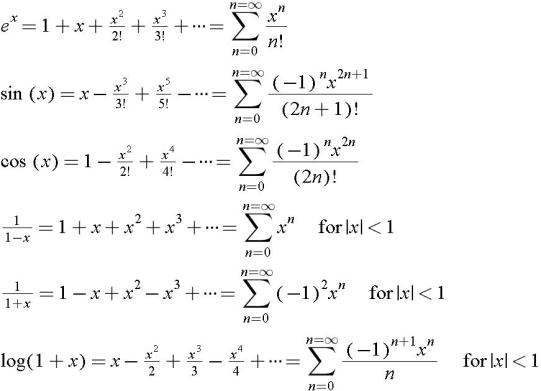
Appendix C Expansions Differentiation Integrals And Mathematical Relations Engineering360

Video 2737 Power Series Representation Of Ln 1 X Part 2 2 Youtube

Incoming Term: log(1+x) power series,